決定分析(12)-モンティ・ホール問題-
NPO法人日本交渉協会理事 窪田恭史
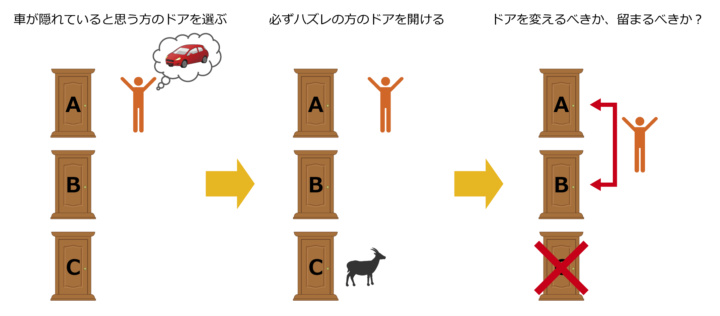
ベイズの定理と直感的な推論がずれることの有名な例に、「モンティ・ホール問題」と呼ばれるパラドックスがある。モンティ・ホールとは、“Let‘s Make a Deal”というアメリカのバラエティ番組の司会者の名前であり、同番組を例にした以下のような問題である。読者は選んだドアを変えるだろうか?それとも、そのままにするだろうか?理由も含めて考えてみてほしい。
問.参加者の前に閉まった3つのドアがあり、1つのドアの後ろには賞品の新車が、2つのドアの後ろには、ハズレを意味するヤギがいる。参加者は新車のドアを当てると新車がもらえる。参加者が1つのドアを選択した後、司会のモンティが残りのドアのうち、ヤギがいるドアを開け、ヤギを見せる。
ここで参加者は、最初に選んだドアを、残る開けられていないドアに変更してもよいと言われる。参加者はドアを変更すべき(switch)か、とどまるべき(stick)か?
1990年、コラムニストのマリリン・ボス・サヴァントが、ニュース雑誌“Parade”連載のコラム「マリリンにおまかせ」で、「正解は『ドアを変更する』である。なぜなら、ドアを変更した場合には景品を当てる確率が2倍になるからだ」と回答し、大騒動に発展した。読者から「彼女の解答は間違っている」と約1万通の投書が殺到し、中には1000人近い博士号保持者が含まれていたという。
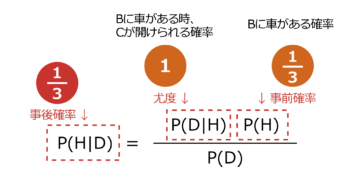
この問題をベイズの定理を使って解いてみよう。簡単にするため、ここでは分母P(D)を無視している。
まず、ドアCが開けられた時、ドアAに車がある確率を求める。ドアAに車がある事前確率は1/3である。Aに車があるとすれば、モンティはドアBかドアCを空けるので、ドアCが開けられる確率(尤度)は1/2である。データの起こる確率P(D)=1なので、ドアAに車がある事後確率は1/6となる。

次に、ドアCが開けられた時、Bに車がある確率、つまりドアAからドアBに変更した場合の確率を求める。ドアBに車がある事前確率は同様に1/3である。Bに車があるとすれば、モンティは必ずドアCを開けるはずなので、ドアCが開けられる尤度は1である。P(D)=1なので、ドアBに車がある事後確率は1/3となる。マリリンの言うとおり、ドアBに変更した方が、車の当たる確率は二倍になるのだ。
AかつBが起こる確率=Aの下でBが起こる条件付き確率×Aの起こる確率
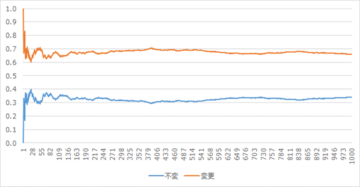
【図1】勝率の推移
【図1】は、モンテカルロシミュレーションを用いて、モンティ・ホール問題を1,000回試行した結果である。1,000回目の変更と不変の勝率の比は1.95:1であった。つまり、変更した場合の勝率はほぼ2倍ということである。モンティ・ホール問題が示すように、人間の認知は確率判断が苦手である。ベイズの定理は、そうした認知の弱点を補うのに役立つであろう。次回は、確率判断における幾つかの認知バイアスについて見ていこう。
参考:
涌井貞美著、『図解・ベイズ統計「超」入門』(サイエンス・アイ新書)
渡辺隆裕著、『ゼミナール ゲーム理論入門』(日本経済新聞出版社)
マックス・H. ベイザーマン著、『行動意思決定論‐バイアスの罠』(白桃書房)
窪田 恭史氏
ナカノ株式会社 取締役副社長
日本繊維屑輸出組合理事
日本交渉協会燮会幹事
日本筆跡心理学協会、筆跡アドバイザーマスター
早稲田大学政治経済学部卒。
アンダーセンコンサルティング(現アクセンチュア)における
コンサルティングおよび研修講師業務を経て、衣類のリサイクルを85年手がけるナカノ株式会社に入社。
現在、同社取締役副社長。
2012年、交渉アナリスト1級取得。
日本交渉協会燮会幹事として、交渉理論研究を担当。
「交渉分析」という理論分野を日本に紹介、交渉アナリスト・ニュースレターにて連載中。
その他のレクチャー