窪田恭史氏による交渉学Web講座

NPO法人日本交渉協会理事 窪田恭史

２．ディシジョン・ツリーの階層構造

下のQ3、Q4について見てみよう。期待効用理論で考えれば、AとB、CとDの確率的利得の比率は、共に16:15である。つまり、選択されるのはAとC、BとDのいずれかであるのが合理的である。そして、期待値はAとCがいずれも高いので、AとCが合理的選択となる。ところが、実験結果はBとCであり、しかもQ3では80％という圧倒的比率でBが選ばれた。考えられるのは、Q3については前回同様、損失回避性により確実な方が選ばれたということ、Q4についてはどちらも当たる確率が低く、両者の確率の差も大きくないので、そうであれば金額の大きい方に賭けてみようというものだ。

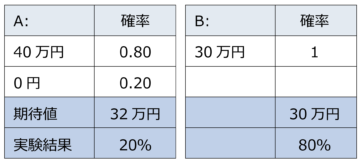
【Q3】

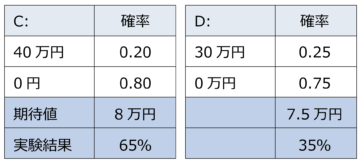
【Q4】

【図1】は、Q4のディシジョン・ツリーである。□は決定ノード、〇は自然の選択により確率的に結果が決まる。つまり、意思決定者が自分の意思で選択できるのは、最初の決定ノードの部分だけである。

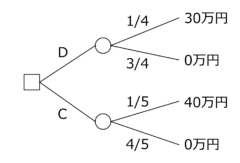
【図1】Q4のディシジョン・ツリー

このツリーを図2のように書き換えてみる。今度は決定ノードより先に確率ノードが来ているが、Q4において、CとDいずれを選択した場合であっても、少なくとも3/4の確率で外れ（利得0円）となる。従って、意思決定者が決定を行わなければならない状況になる（つまり図2の決定ノードに進む）確率は1/4である。この1/4の確率で意思決定者がDを選択すれば30万円が得られ、Cを選択すれば、さらに4/5の確率（つまり合計1/5の確率）で40万円が得られる。しかし、Cの場合は1/5の確率（合計1/20の確率）で外れの可能性もある。

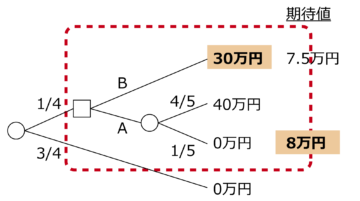
【図2】Q4のディシジョン・ツリー②

重要なのはここからである。図2を見ると、ディシジョン・ツリーの下位の木、赤い点線で囲まれた部分は、Q3のディシジョン・ツリーと同じなのである。図2において、最初の確率ノードは自然の選択であるので、意思決定者の選択は介在しない。3/4の確率で0円となれば、自動的にそこで終了である。つまり、Q4において選択を行うには、1/4の確率で赤点線枠内の決定ノードに進むことが条件なのだ。ということは、Q３とQ4の意思決定は同じものなのである。同一の決定であれば、選択はAとC、BとDのいずれかでなければならない。Q３では圧倒的比率でBが選択され、しかも同一の決定であるはずなのにQ4ではCが選択され、しかもその割合がQ3に比べると65％と控えめであるのは、明らかに不合理なのだ。

3．共通比率効果

今度は以下のQ5、Q6でそれぞれどちらを選択するだろうか？

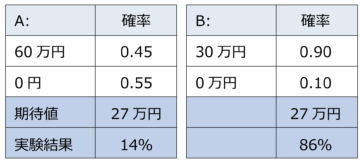
【Q5】

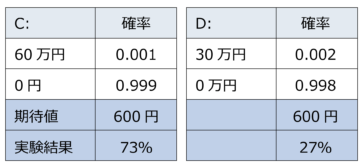
【Q6】

期待効用理論では、Q5のAとBの期待値は共に27万円、Q6のCとDの期待値は共に600円、つまりいずれも無差別である。ところが実験結果は、Q5では圧倒的多数の86％がBを選択し、Q6でもやはり多数がCを選択した。これまでのように、Q5におけるBの選択の理由が損失回避性にあるのであれば、Q6ではDが選択されないのか？カーネマンらによれば、その理由は確率があまりに低いので、人はその違いを無視しがちだというものである。これを「共通比率効果」といい、前節のQ4についても当てはまる。

参考：
M. Grauer et al. (eds.)　(1985) Plural Rationality and Interactive Decision Processes, p.100-113 “Back from Prospect Theory to Utility Theory”