窪田恭史氏による交渉学Web講座

NPO法人日本交渉協会理事 窪田恭史

ある事象Aが起こったという条件のもとでの事象Bの確率（条件付き確率）が成り立つ定理を「ベイズの定理」といい、18世紀の数学者、トーマス・ベイズによって示され、その後、ラプラスによって再発見・発展した。意思決定論とは、ある情報を得て次にどの行動をとるのが最善かを決める理論のことであるが、その決定にベイズの定理を用いた意思決定をベイズ的意思決定という。

ライファは1957年、コロンビア大学からハーバード大学へ移った。そこでのキャリアのスタートは、ロバート・シュレイファー、ジョン・プラットとの統計的決定論の共同研究であった。『応用統計的決定論』（ライファとシュレイファー、1961）と『統計的決定論入門』（プラットら、1965）は、標準的な統計的問題にベイズ論的分析の基礎を与えたものである。つまりライファは早くからベイジアンだったのであり、必然的に”Negotiation Analysis”には、このベイズ論的な考え方が前提として置かれている。したがって、”Negotiation Analysis”を理解するには、まずベイズ理論の基本に触れておくことが欠かせない。涌井貞美著、『図解・ベイズ統計「超」入門』は数式を使わず、図解でベイズ理論の基本を分かりやすく解説している。以下、ベイズ的意思決定については、基本的に同書からの引用で話を進めていく。

初めに、ベイズの定理を理解す上での基本概念、「同時確率」、「条件付き確率」、「乗法定理」、「加法定理」について見ていこう。

1．同時確率＜P(AB)＞

事象Aかつ事象Bが起こる確率のことを「同時確率」という。例えば、ジョーカーを除くトランプの山から1枚引いた時に、カードがハートかつ絵札である確率。つまり、ハートかつ絵札の同時確率は3/52である。

2．条件付き確率＜(B|A)＞

事象Aが起こった時に、事象Bの起こる確率のことを「条件付き確率」という。例えば、抜いたカードがハートであった時に、絵札であるという条件付き確率は、3/13である。

3．乗法定理＜P(AB)=P(B|A)P(A)＞

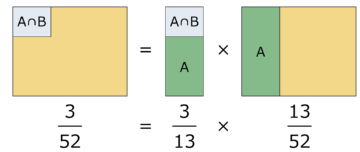
AかつBが起こる確率=Aの下でBが起こる条件付き確率×Aの起こる確率

同時に起こる確率は、各々の確率の積になる。これを「乗法定理」という。例えば、ジョーカーを除くトランプの山から1枚引いた時に、カードがハートかつ絵札である確率。前述のように、ハートかつ絵札である確率は3/52であるが、これは分解すれば、カードがハートであった時に、絵札であるという条件付き確率、3/13とカードがハートである確率、13/52の積である。

4．加法定理＜P(A∪B)=P(A)+P(B)＞

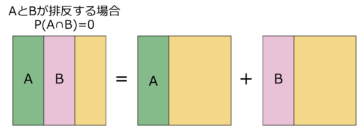
AまたはBの起こる確率=Aの起こる確率+Bの起こる確率

AとBが同時に起こることがない（排反する）時、「加法定理」が成立するという。上図を見れば分かりやすいが、AとBが排反するのであれば、AまたはBの起こる確率はAの起こる確率＋Bの起こる確率である。

5．ベイズの定理

「ベイズの定理」とは、簡単に言えばAの下でBが起こる条件付き確率をBの下でAが起こる条件付き確率との関係から表した定理である。乗法定理より、

である。P(AB)とP(BA)は同じことであるので、

即ち、Aの下でBが起こる条件付き確率は、P(A) > 0 のとき次が成り立つ。

これがベイズの定理である。今後の理解を容易にするため、Aを仮定（H）、Bを仮定から得られるデータ（D）と置き換える。

P(H)を事前確率、P(H│D)を事後確率、P(D│H)を尤度という。尤度とは、「もっともらしさ」という意味である。ベイズの定理は、意思決定者が情報を得る前の確率的推測（事前確率）が、情報を得た後にどのように更新されるか（事後確率）を示した定理であり、不確実性の意思決定における確率的推測で中心的役割を果たしている。

参考：
Ralph L. Keeney (2016) Remembering Howard Raiffa. Decision Analysis 13(3):213-218
涌井貞美著『図解・ベイズ統計「超」入門』（サイエンス・アイ新書）
上田泰著『文科系のための意思決定分析入門』（日科技連）
渡辺隆裕著『ゼミナール　ゲーム理論入門』（日本経済新聞出版社）