窪田恭史氏による交渉学Web講座

NPO法人日本交渉協会理事 窪田恭史

1.アレのパラドックス

前回述べたように、期待効用理論は現実の人間の行動を説明するものではないとする批判も多い。その先鞭ともいえるのが、「アレのパラドックス」である。1988年にノーベル賞を受賞した、経済学者のモーリス・アレは、1953年にニューヨークで行われた会議において、以下のような実験を行い、実際の人間が期待効用理論には従わないということを示した。

1回目の実験。今、2つのくじA1とA2がある。A1は確実に100万ドルがもらえる。一方、A2は0.10の確率で500万ドル、0.89の確率で100万ドルが当たり、0.01の確率ではずれとなる。この時、500万ドルの効用を1.0、0ドルの効用を0とし、100万ドルの効用は0と1.0の間の任意の値Zであるとする。実験1では、ほとんどの人が確実に100万ドルをもらえるA1を選択した。

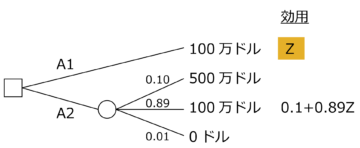
【図1：1回目の実験】

２回目の実験では、2つのくじA3とA4がある。A3は0.10の確率で500万ドルがもらえるが、0.90の確率ではずれとなる。A4は0.11の確率で100万ドルがもらえるが、0.89の確率ではずれとなる。2回目の実験では、ほとんどの人がA3を選択した。

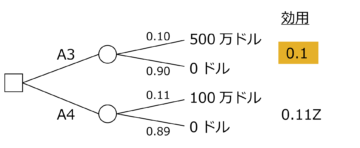
【図2：２回目の実験】

しかし、期待効用理論に照らせばこれはおかしい。なぜなら、A2よりA1を選択するのは、Z>10/11（≒0.9）の時である。そうであれば、2回目はA3ではなくA4が選択されなければならない。ところが、アレの実験の結果、ほとんどの人はA1とA3を選択し、期待効用理論に基づく結果を知らされた後でさえも変えたがらなかったという。

1979年に論文で期待効用理論に代わるものとして「プロスペクト理論」を提唱した、ダニエル・カーネマンとエイモス・トヴェルスキーによれば、1回目の実験結果は、確率が0％もしくは100％などの確実性の高いものに価値を感じる、「確実性効果（certainty effect）」として説明される。また、2回目の実験結果のように、非常に小さい確率を無視する傾向のことを「共通比率効果」と呼んでいる。こうした心理効果があるために、現実の人は効用最大化を目指すようには行動しないというのである。

2.エルスバーグのパラドックス

もう1つ、「ペンタゴン・ペーパーズ」で一躍有名となったダニエル・エルスバーグは、1961年の論文の中で、確率が未知であるような事象を回避しようとする選好（曖昧さ回避）の具体例を挙げ、期待効用理論が現実の意思決定を十分に反映したものではないことを示した。因みにライファは、エルスバーグの指導教授でもある。

エルスバーグの示したパラドックスとは，次のようなものである。上図のような2つの壺があり、壺Aには赤玉が50個、白玉が50個入っていることが分かっている。もう一方の壺Bには、赤玉と白玉が入っていることは分かっているが、その数は分からない。今、事前に赤玉と白玉のどちらを引くかを宣言し、見事引き当てたら賞金100ドルがもらえるとする。あなたはAとBの壺どちらを選ぶだろうか？

大抵の人は壺Aを選ぶと回答する。ではその人たちに、壺Bに入っている赤玉と白玉に優劣はあるかと尋ねると、大方の人は「優劣はない」と回答したという。優劣がないのであれば、壺Bの赤玉を引く確率と白玉を引く確率は等しいはずである（PB(R)＝PB(W)）。

壺Aの赤玉と白玉を引く確率は五分五分なので、PA(R)＝0.5　PA(W)＝0.5である。壺Bより壺Aを選ぶのであれば、PA(R)＞ PB(R)、 PA(W)＞ PB(W)かつPA(R)＋ PA(W) ＞ PB(R)＋PB(W)でなければならない。ところがこれでは、PA(R)＝0.5　PA(W)＝0.5なので、１＞ PB(R)＋PB(W)となってしまい、「加法性」（確率の合計は１になる）という期待効用理論の重要な原則に反することになってしまうのである。これがエルスバーグのパラドックスである。

3.プロスペクト理論

前述のように、カーネマンとトヴェルスキーは、期待効用理論に代わるものとして「プロスペクト理論」を提唱した。この理論の特徴は、期待効用理論とは異なり、1．人々は提示された確率に対して非線形に反応していると主張していること、そして2．人々は利得と損失を異なるように扱うと主張していることである。彼らは前者を「確率加重関数」として、後者を効用関数に代わる「価値関数」として説明している。

3.1．確率加重関数
期待効用理論において、確率は線形的である（例えば確率50は確率100の1/2）。しかし、カーネマンらによれば、主観的確率は、実際とはズレがあり、人は、小さい確率を過大評価し、大きな確率を過小評価する傾向がある。言い換えれば、確率が小さい時、人はリスク回避的に行動し、確率が大きい時、リスク愛好的に行動する傾向がある（図3）。

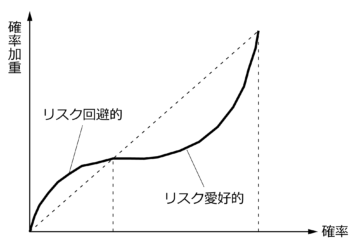
【図3：確率加重関数】

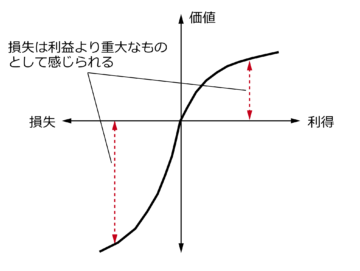
【図4：価値関数】

関数のグラフが非線形であるのは、確率自体に意思決定者の「思い」を加重されているためである。これを「確率加重」という。

3.2．価値関数
カーネマンらは、効用関数に代わるものとして、「価値関数」を提唱した。人は「参照点」と呼ばれる貨幣を比較するための基準点を個々に持っており、参照点よりも高ければ利得として、低ければ損失として認識する。図4のように、価値関数の曲線は効用曲線と異なり、損失はリスク愛好的に、利得はリスク回避的に描かれる。これは、人には、「損失回避性」があり、損失を認識すると、利得よりも重大なものとして捉える傾向があるためである。これを「損失と利得の非対称性」という。また、利得をリスク回避的に、損失をリスク愛好的に評価する傾向を「反射効果」という。なお価値関数は、貨幣の絶対水準ではなく、参照点からの変化を表しているのだという点に注意が必要である。

以上、期待効用理論に対する様々な批判を見てきた。ライファはこれらの批判を認めた上で、それらは現実の人間行動を記述するには優れているが、より良い意思決定を行うという目的においては、依然として期待効用理論が望ましいのではないかと考えていた。1985年の論文、”Back From Prospect Theory To Utility Theory”の中で、ライファはカーネマンらの実験を再現しつつ、期待効用理論に基づく規範を提示している。これらについて、次回以降見ていこう。

参考：
Howard Raiffa John Richardson David Metcalfe（2002）Negotiation Analysis: The Science and Art of Collaborative Decision Making
マックス・H. ベイザーマン著、『行動意思決定論‐バイアスの罠』（白桃書房）
イツァーク・ギルボア著、『意思決定理論入門』（NTT出版）