決定分析(9)-効用理論に戻れ(1)-
NPO法人日本交渉協会理事 窪田恭史
前回も述べたように、ライファはカーネマンやトヴェルスキーの主張するプロスペクト理論を否定してはいない。期待効用理論が現実の人間行動を上手く記述できないことも認めており、”Negotiation Analysis”の中でも行動意思決定論の研究成果をしばしば取り上げている。それでもライファは、より良い意思決定を行う手法として期待効用理論は依然として有用であると考えており、1985年に”Back from Prospect Theory to Utility Theory”という論文を著している。交渉分析において、交渉相手の行動や戦略を記述的に説明したり予測したりするには、行動意思決定的分析が優れており、その上で交渉当事者が意思決定の処方を下すための規範を示すのには従来の決定分析が優れていると、それぞれ役割が異なるとライファは考えていた。
“Back from Prospect Theory to Utility Theory”において、ライファはカーネマンとトヴェルスキーによる幾つかの実験を自らの生徒を対象に再現し、その結果と共にプロスペクト理論が指摘する現実の人間による合理性からの逸脱に対する規範を示している。ライファは、そもそも人間が規範的であるなら、より賢明な意思決定を行うために主観的期待効用理論で規範を示す理由はないと述べている。ここでは、同論文を元に、カーネマンらが主張した、損失回避性、共通比率効果、反射効果、そしてディシジョン・ツリーの階層構造について採り上げる。
1.損失回避性
人は目の前に利益については、それが手に入らないリスクの回避を優先し、目の前の損失については、それを回避しようとする傾向がある。この傾向故に、現実の人は期待効用理論の説く効用最大化と合致しない行動を取る。
次の二つの選択肢AとBから一つを選ぶとしたら、どちらを選ぶだろうか?つまり、Aは33%の確率で25万円もらえ、66%の確率で24万円がもらえる。ただし、1%の確率で何ももらえない。一方Bは、確実に24万円が手に入る。
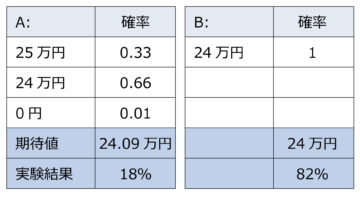
【Q1】
期待効用理論では、AとBの期待値はそれぞれ24.09万円と24万円ということになり、Aを選択するのが合理的ということになる。ところが、実際の実験結果(72名)では実に82%の学生がBを選択したのである。これが損失回避性と呼ばれる現象である。
では、次のQ2はどうか?
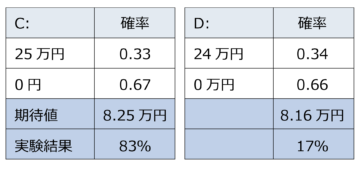
【Q2】
今、0円の効用u(0円)=0、25万円の効用u(25万円)=1、24万円の効用u(24万円)=Xとすれば、0≦X≦1の時、
X>33/34なら、A≺BかつC≺D
X<33/34なら、A≻BかつC ≻D
X=33/34なら、A~BかつC~D
となる。A≺Bは「BをAより好む」、 A~Bは「AとBは無差別(差がない)」という意味である。つまり、Q1でAよりBを好むのであれば、Q2でもCではなくDが選択されなければならない。ところが現実の学生は、Q2では83%がCを選択したのである。このように現実の人間は損失回避性ばかりでなく、推移性にも従わない場合がある。つまり、意思決定に一貫性がないのである。
しかし、このQ1とQ2の選択を以下のような例に置き換えて考えてみよう。「24万円」というラベルを貼った赤玉66個と白玉34個の入った壺があるとする。今、このうち白玉33個のラベルを「25万円」に張り替え、残る1個の白玉についてはラベルをはがす(つまり、0円)とする。ラベルを貼りかえる前は、Q1の選択肢Bの状況と同じであり、ラベルを貼りかえた後は選択肢Aと同じ状況である。前者をつぼB、後者をつぼAとすると、つぼAもBも24万円の赤玉66個が入っている状況は同じなので、比較の対象はつぼAには25万円の白玉33個、0円の白玉1個であるのに対して、つぼBは24万円の白玉34個ということになる。読者の皆さんであれば、どちらのつぼを選ぶだろうか?つぼAの方が良いと考えた方も多いのではないだろうか?

【Q1】
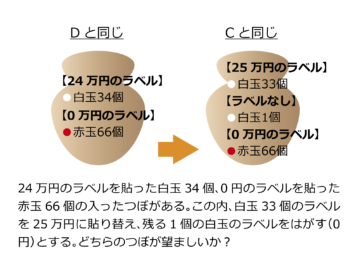
【Q2】
Q2も同様である。「24万円」のラベルを貼った白玉34個と「0円」のラベルを貼った赤玉66個が入っているつぼDと、ラベルを貼り替え、「25万円」の白玉33個と「0円」の赤玉66個、そしてラベルをはがした(0円)白玉1個のつぼCとどちらを選ぶだろうか?比較の対象はつぼCが、「25万円」の白玉33個とラベルをはがした(0円)白玉1個、つぼDが「24万円」の白玉34個である。つぼCの方が良いと考えた方も多いのではないだろうか?もし、つぼAとつぼCが望ましいと考えたなら、それは期待効用理論と合致しているのである。
「そんなことはない。自分はもしつぼAを選んで0円の白玉を引いてしまったら、何故確実なつぼBを選ばなかったのだろうときっと後悔するだろう。周りの人からバカだと思われるかもしれない。後悔だけでなく、選ぶ前でも『もし0円の白玉を引いてしまったら』という不安が拭えない」と言う人もいるかもしれない。ライファは問う、「では、その不安を拭い去れるとしたらいくら払うか?」と。仮にその不安は金額にして5千円に相当するとしよう。しかし、つぼAにおいて0円の白玉を引く確率は1/100である。即ち、事後するかもしれない後悔は5千円×0.01、わずか50円に過ぎないのだ。仮に事前の不安が1万円に相当するとしても、やはり事後の後悔は100円に過ぎない。そればかりの損失を恐れて、1万円多く得られる確率が33%もあり、24万円以上得られる確率が99%の選択肢を回避するのは大げさ過ぎるのではないか、というのがライファの主張である。
参考:
M. Grauer et al. (eds.) (1985) Plural Rationality and Interactive Decision Processes, p.100-113 “Back from Prospect Theory to Utility Theory”
窪田 恭史氏
ナカノ株式会社 取締役副社長
日本繊維屑輸出組合理事
日本交渉協会燮会幹事
日本筆跡心理学協会、筆跡アドバイザーマスター
早稲田大学政治経済学部卒。
アンダーセンコンサルティング(現アクセンチュア)における
コンサルティングおよび研修講師業務を経て、衣類のリサイクルを85年手がけるナカノ株式会社に入社。
現在、同社取締役副社長。
2012年、交渉アナリスト1級取得。
日本交渉協会燮会幹事として、交渉理論研究を担当。
「交渉分析」という理論分野を日本に紹介、交渉アナリスト・ニュースレターにて連載中。
その他のレクチャー